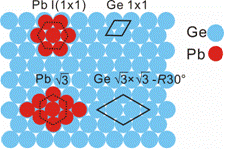
Fig. 1 Schematic diagrams for
the Ge(111)-(1¡Ñ1) substrate
surface,
a Ge(111)-(1¡Ñ1) unit
cell,a Ge(111)-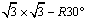 unit
cell, a Pb unit
cell, a Pb
I(1¡Ñ1)domain, and a
Pb
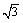 domain. domain.
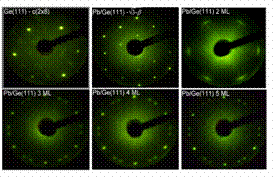
Fig. 2 LEED patterns, taken
with the beam energy at 40 eV, from
Ge(111)-c(2¡Ñ8), Pb/Ge (111)-
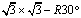 b
phase, and 2, 3, 4, b
phase, and 2, 3, 4,
and 5 ML of Pb overlayers.
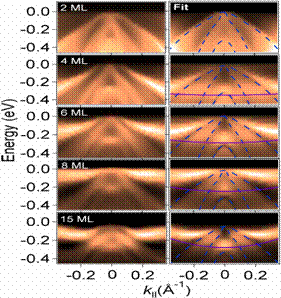
Fig. 3 Left panel:
angle-resolved photoemission
results along
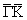
for Pb film thicknesses of 2, 4, 6,
8, and 15 ML. Right panel: model
fits to the data. The dashed
curves indicate the Ge band
edges.The
solid curves indicate
QWS subbands from the fits. |
¡@ |
It has been a long-standing
puzzle for years that metal films can grow smoothly on semiconductor
surfaces, retaining its own lattice constant, in spite of large lattice
mismatch [1, 2, 3, 4]. In the past, scientists have either overlooked
the reason or naively assumed that the large lattice mismatch caused the
metal films to be free-standing-film-like. In a recent Phys. Rev. Lett.
paper [5], Shu-Jung Tang of
TUNational Tsing Hua UniversityUT,
TUHsinchuUT,
TUTaiwanUT
and co-workers reported the discovery of an important clue to this
puzzle by investigating the system of Pb films on Ge(111). They showed
that the growth of an incommensurate (1¡Ñ1) parallel-epitaxy
configuration is bound to another mysterious driving force for the
epitaxial growth: electronic match. The perfect electronic match would
cause the maximum hybridization between the quantum-well states (QWS) of
the metal films and band edges of the semiconductor substrate so as to
reduce the energy of the system.
The mismatch between the Pb
and Ge lattice constants, 4.92 Å and 5.65 Å, is 13%. However, if the Pb
film is rotated by 30º from the I(1¡Ñ1) configuration, the Pb (2¡Ñ2) unit
cell and the substrate 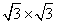 unit
cell become well
matched (Fig. 1). unit
cell become well
matched (Fig. 1).
¡@
Low energy electron diffraction (LEED) measurements reveal the film
growth orientation (Fig.2). Patterns from the bare Ge(111)-c(2¡Ñ8) and
the Pb/Ge(111) -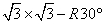 b
phase establish the reference orientations and
scale factors. Upon Pb coverage at 2 monolayers (ML),
the b
phase establish the reference orientations and
scale factors. Upon Pb coverage at 2 monolayers (ML),
the 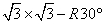 pattern
is suppressed. An attenuated Ge(111)-(1¡Ñ1) substrate pattern remains and
is accompanied by six short arcs with the same orientation but farther
out. The radius of the arcs indicates an I(1¡Ñ1) Pb overlayer. Also
evident in the data is the emergence of pattern
is suppressed. An attenuated Ge(111)-(1¡Ñ1) substrate pattern remains and
is accompanied by six short arcs with the same orientation but farther
out. The radius of the arcs indicates an I(1¡Ñ1) Pb overlayer. Also
evident in the data is the emergence of
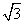 domains
at 3 ML which eventually dominates at higher Pb coverages . Angle-resolved
photoemission mapping of Pb overlayers of thicknesses 2, 4, 6, 8, and 15
ML along the domains
at 3 ML which eventually dominates at higher Pb coverages . Angle-resolved
photoemission mapping of Pb overlayers of thicknesses 2, 4, 6, 8, and 15
ML along the 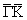 direction
yield spectral functions shown in Fig. 3.
At 2 ML, the results closely resemble the k-resolved
one-dimensional density of states of the Ge bulk band structure because
of a strong hybridization of the
Pb and Ge states and the large contribution from the Ge states within
the photoemission probing depth
[6]. direction
yield spectral functions shown in Fig. 3.
At 2 ML, the results closely resemble the k-resolved
one-dimensional density of states of the Ge bulk band structure because
of a strong hybridization of the
Pb and Ge states and the large contribution from the Ge states within
the photoemission probing depth
[6].
The data at higher coverages (4-15 ML) in Fig. 4 are quite different; an
Anderson model involving a hybridization interaction of the discrete Pb
QWS subbands and the Ge states [5] is used to construct a model spectral
function. The solid purple curve shows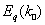 ,
the dispersion of the "bare" QWS subband. ,
the dispersion of the "bare" QWS subband.
Two competing factors are
at play: one is the interfacial energy, which is independent of the film
thickness and favors the 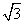 lattice-matched
configuration, and the other is the electronic energy associated with
quantum confinement, which diminishes as 1/N and also depends on
the degree of electronic hybridization across the Pb-Ge interface. A
strong hybridization as a result of electronic match minimizes the
effects of confinement, leading to a lower system energy. The authors convincingly
argue that the I(1¡Ñ1) configuration presents a much better electronic
match than the lattice-matched
configuration, and the other is the electronic energy associated with
quantum confinement, which diminishes as 1/N and also depends on
the degree of electronic hybridization across the Pb-Ge interface. A
strong hybridization as a result of electronic match minimizes the
effects of confinement, leading to a lower system energy. The authors convincingly
argue that the I(1¡Ñ1) configuration presents a much better electronic
match than the 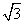 configuration
based on general symmetry considerations. Thus, the I(1¡Ñ1) configuration
is preferred at small thicknesses for Pb/Ge(111). configuration
based on general symmetry considerations. Thus, the I(1¡Ñ1) configuration
is preferred at small thicknesses for Pb/Ge(111).
The general understanding
established in Tang,
et al. [5], is
important for devising strategies for smooth film growth with prescribed
configurations ¡V a key issue relevant to thin film electronics. |



